
Liliana Caycedo Lozano 1 y Jeannette Vargas Hernández 1
1 Programa de Ciencias Básicas, Universidad Colegio Mayor de Cundinamarca, Bogotá, Colombia.
Recibido: 07-06-03; Aceptado: 12-11-03
Existen conceptos que se emplean cotidianamente, como es el de «medir»; tal vez, por ello, el sistema educativo tangencialmente delega a dicha cotidianidad la responsabilidad de la práctica y experimentación. Sin embargo, se evidencia que en la educación universitaria difícilmente se puede trabajar en la formalización del concepto “medir” sin antes haber generado los espacios para experimentar y analizar los procesos de medición de algunas magnitudes. Es por ello que se plantea una propuesta de talleres previos que tengan en cuenta esa necesidad y posibiliten una aplicación directa a la química.
Palabras Claves: Proceso pedagógico, medición de magnitudes.
A proposal with students of Bacteriology: How to approach the process of measuring magnitudes experimentally?
There areconcepts that we daily use, as the act of measure, and perhaps, for that reason, our educational system gives to that act day to day the act responsibility of its practice and experimentation. However, it is clear that in the higher education one hardly can work in the formalization of the “measurement” concept without have before created the space for the analysis and experimentation of the measurement process of some magnitudes. In order to improve this behavior we are here proposing to carry out previous workshop to take into account the above mentioned problem need and make a direct application to the Chemistry possible.
Keywords: Pedagogic process, mensuration of magnitudes.
En el primer semestre de 1999 en la asignatura Matemática, al iniciar la unidad denominada “Sistemas de Medida” se solicitó a los estudiantes realizar la lectura titulada “Medición”, del tomo No. 5 de la colección Sigma. Una vez realizada esta lectura, los estudiantes solucionaron un taller sobre medidas de longitud tomado del libro de texto de Geometría 6º de la serie Actividad Matemática, el cual presenta objetivos, materiales y cada uno de los pasos que deben llevar a cabo los estudiantes para determinar la distancia entre dos puntos de una recta.
Posterior a este trabajo, se presentó un cuestionario a 40 estudiantes con la pregunta: «¿A qué llamas medir?», y se clasificaron las respuestas en seis categorías que obtuvieron los porcentajes relacionados en la Tabla 1.
Tabla 1. Categorías y porcentajes de respuestas.

En la categoría 1 se observa que se omite la unidad que permitiría la asignación del número y tampoco se enuncia mediante qué proceso se efectuaría dicha asignación.
La categoría 2 tampoco enuncia explícitamente que existe un proceso para la asignación del número, sin embargo, puede estar implícito en el momento en que hacen referencia a una unidad patrón.
En la categoría 3 la palabra “calcular” conduce a pensar en un proceso de aplicación de fórmulas, sin dejar ver qué aspectos los estudiantes consideran relevantes de la medición.
En la categoría 4 se explica la medición como un proceso de comparación; sin embargo, no hacen alusión a la magnitud que va a ser medida ni al resultado final de dicha comparación.
La categoría 6 es la que más elementos del concepto de medición posee, ya que hace alusión al proceso de comparar la necesidad de una unidad patrón y el resultado de dicho proceso.
De la socialización de estos resultados por parte del profesor de matemáticas con los docentes de química, surgió en uno de ellos la inquietud de efectuar una exploración con las estudiantes de primer semestre, en la misma temática de medida, en la unidad denominada “Fundamentos de la Química”, con el fin de observar si existía la presencia de dificultades similares; en otro grupo de primer semestre del mismo programa, el docente en la asignatura de Química I, efectuó una exploración alrededor de la misma temática.
Las inquietudes alrededor de la temá- tica de medida que dieron origen a esta experiencia surgieron de la práctica docente. En el trabajo en el aula se detectaron dificultades que, al ser analizadas tenían como punto de intersección la noción de medición; los docentes de matemáticas y química diseñaron talleres y cuestionarios que posibilitaron otra forma de abordar dicha temática. Por ello se considera que tanto este análisis de dificultades como las estrategias para abordarlas, se pueden caracterizar como un proceso de “indagación-práctica”, cuya preocupación central es encontrar soluciones concretas a los problemas que se presentan en la realidad cotidiana.
En el primer semestre del año 2000, en la asignatura de Química I, antes de iniciar esa temática se llevó a cabo un sondeo a 126 estudiantes, centrado en un cuestionario que contenía las siguientes preguntas:
1. ¿Qué es medir?
2. ¿Qué es un patrón de medida?
3. ¿Qué sistemas de medida conoce usted?
4. ¿Qué es volumen?
5. ¿Ha trabajado con factores de conversión?
6. ¿Qué entiende por exactitud y precisión?
Con la información obtenida se llevó a cabo una clasificación de la siguiente manera:
En las respuestas clasificadas en la tabla 1, los estudiantes asocian el concepto de medir con una sola acción; observar, calcular o comparar, no explicitan y resulta difícil interpretar si estas palabras están asociadas a un proceso y qué tipo de proceso. ¿Es sólo percepción?, ¿es la aplicación de fórmulas?
Tabla 2: Respuesta a la pregunta ¿Qué es medir?

Tabla 3: Respuesta a la pregunta ¿Qué es un patrón de medida?

Tabla 4: Respuesta a la pregunta ¿Qué sistemas de medida conoce usted?

Tabla 5: Respuesta a la pregunta ¿Qué es volumen?

Tabla 6: Respuesta a la pregunta ¿Ha trabajado con factores de conversión?

Tabla 7: Respuesta a la pregunta ¿Qué entiende por «exactitud» y «precisión»?

Las respuestas de las tablas 3 a la 6 están íntimamente ligadas, dejando entrever el desconocimiento sobre lo que es un patrón de medida, sistemas de medida y factores de conversión. En la Tabla 7 es evidente que no existe un acercamiento a conceptos como exactitud y precisión que son inherentes a la medición.
De la clasificación obtenida, una de las conclusiones que se puede establecer es que a pesar del recorrido académico de los estudiantes, no se evidencia una conceptualización alrededor de la temática de medición, es decir, las experiencias con longitud, superficie, volumen, tiempo, etc., no se han integrado en una red conceptual que le permita al estudiante generalizar un significado de dicho concepto.
Atendiendo a las anteriores observaciones elaboradas por los docentes en las asignaturas de Matemáticas y Química I en la Universidad Colegio Mayor de Cundinamarca, se decidió organizar el contenido de esta unidad en dichas asignaturas, centrando el interés en la comprensión del proceso de asignación de un número para representar la magnitud e identificar diversos pasos que intervienen en este proceso.
En dicha organización del contenido de las dos asignaturas, en lo que respecta a Matemáticas, se conservó la estrategia de invitar a los alumnos a acercarse al significado de medir magnitudes a través de la lectura “Medición” ya mencionada. Para facilidad del lector se transcriben apartes del texto:
MEDICIóN- por Norman Campbell
¿Qué es medición? : La medición puede definirse en general como la atribución de números a propiedades, para representarlas.
Lo primero que me interesa subrayar es que no todas las propiedades pueden representarse mediante números, sino solo algunas de ellas.
Para poder apreciar por qué es tan importante esa diferencia, tenemos que penetrar más profundamente en la significación del “número”. Tenemos que observar que es muy fácil que se produzca confusión en este punto, pues la palabra “número” se usa para un mero nombre, palabra o símbolo, y a veces significa una propiedad de un objeto.
Las propiedades medibles de un cuerpo son aquellas que cambian por la combinación de cuerpos semejantes; las propiedades no medibles son las que no cambian al realizar esta operación.
¿Qué propiedades son medibles?: Para que una propiedad sea medible debe ser tal que:
1. Dos objetos que respecto de esa propiedad sean lo mismo que un tercer objeto, sean lo mismo el uno que el otro.
2. Por la adición sucesiva de objetos podamos construir una serie normal, un miembro de la cual sea lo mismo, respecto de la propiedad, que cualquier otro objeto que deseemos medir.
3. Iguales añadidos a iguales produzcan sumas iguales.
Con estos acercamientos teóricos y prácticos y rescatando las experiencias que han tenido los estudiantes en su escolaridad, “sin dejar de lado las observaciones detectadas al iniciar”, se solicitó a los grupos que propusieran otro taller que continúa centrado en la medida, orientado hacia las magnitudes volumen y capacidad, las cuales se seleccionaron teniendo en cuenta que son relevantes en los contenidos del currículo de esta carrera de pregrado, debido a que un profesional de bacteriología continuamente hace uso de ellas durante su ejercicio, tanto en lo referente a la literatura científica como al trabajo práctico.
Como parámetros: los alumnos pueden incluir pasos similares a los establecidos en el taller de medida de longitud, por ello deben hacer claridad en los objetos escogidos, la magnitud a medir, la unidad, el proceso de comparación –¿cuántas veces cabe esa unidad?– y, por lo tanto, la asignación de un número, obteniendo un número con la unidad para representar la medida.
Los talleres propuestos por los estudiantes, se clasifican en tres grupos teniendo como punto de referencia el aspecto en el cual hicieron énfasis; aquellos talleres que presentan materiales y pasos alrededor de la actividad de medir con unidades arbitrarias; los otros, alrededor de medir identificando múltiplos y divisores de unidades arbitrarias y un tercer grupo que identifica múltiplos y divisores del sistema métrico decimal.
Taller – Grupo 1. Utilización de unidades arbitrarias
Objetivos: En este taller aprenderás a realizar mediciones de volúmenes teniendo en cuenta los materiales asignados para cada ejercicio, valiéndose de otros objetos.
Materiales: Cubos de cartulina, una caneca, una caja de plástico, cubos de caldo de gallina, una cajita de pasta azul, cajitas de chicles, una cubeta de hielo, cajas de fósforos.
Pasos a seguir:
1. Con los cubos de cartulina mide una caneca que está en la zona verde de la universidad. ¿Cuántos cubos caben en la caneca?
2. En la caja de plástico mide la cantidad de cubitos de caldo de gallina que caben en esta caja.
¿Cuántos cubitos son?
3. Con cajas pequeñas de goma de mascar mide:
a. La cajita de cartón.
b.La cajita de pasta azul.
4. Mide la cubeta de hielo con las cajas de fósforos. ¿Cuántas cajas de fósforos caben en la cubeta?
En el procedimiento anterior has medido volúmenes partiendo del volumen de otros objetos. Para esto utilizaste objetos como cubos, cajas de goma de mascar, de fósforos, para definir diferentes unidades de medida como la caneca, la caja de cartón, la cubeta de hielo.»
A pesar de que en el procedimiento del párrafo anterior se nombra como unidad de medida la caneca, en la parte experimental los estudiantes establecen que las unidades arbitrarias de medida que estaban utilizando eran los cubos, las cajas de goma de mascar, etc., para medir el volumen de la caneca.
«Taller – Grupo 2: Múltiplos y divisores de unidades arbitrarias
Materiales:
Unidades de medida:
Cuchara, pocillo
Unidad de medida referencial:
Copa de aguardiente.
Objetivo : Hallar la capacidad de la copa teniendo en cuenta las unidades de medida, encontrar múltiplos y divisores.
Problema:
¿Cuántas cucharadas puede contener la copa?
¿Cuántos contenidos de la copa puede contener el pocillo?
¿Cuáles son los divisores y los múltiplos?
Resultado:
La copa tiene capacidad para 5 cucharadas. El pocillo tiene capacidad para 5 veces el contenido de la copa. Como se mencionó anteriormente, la copa es la unidad de medida referencial, por lo tanto, le podemos hallar múltiplos y divisores.
Divisor: 1 cucharada es el divisor, porque 5 cucharadas están contenidas en la copa.
Múltiplo: 1 pocillo es el múltiplo, porque 5 veces el contenido de la copa esta contenido en el pocillo.
Taller – Grupo 3: Identificación de múltiplos y divisores de sistema métrico decimal
Un ejemplo de la clasificación de talleres planeados y solucionados por los alumnos, relacionados con el sistema métrico decimal, lo titularon Capacidad y Volumen, y para él presentaron la siguiente estructura:
Objetivo: Diseñar un procedimiento que permita determinar el volumen de los materiales empleados. Adquirir conceptos básicos mediante la práctica.
Relacionar medidas de volumen y capacidad, mediante el empleo de elementos determinados (cubo)
Materiales : Cubo de Vidrio, Cubos de azúcar,
Agua, Vasos, Balanza, Gotero, Botellas, Líquidos
Algunos conceptos
Volumen: Por convención, la unidad de medida para determinar un volumen es la región del espacio ocupada por un cubo, cuya arista mida una unidad de longitud y la llamamos cubo unidad. La “convención” puede provenir de cálculos subsiguientes, pues el volumen del cubo se halla, simplemente, calculando la tercera potencia de la medida de la arista.
La unidad fundamental del volumen en el sistema internacional es el metro cúbico.
El metro cúbico es el volumen que ocupa, en el espacio, un cubo cuya arista mide 1 metro.
Capacidad: Para medir los volúmenes interiores del recipiente destinados a contener líquidos, como tanques, frascos, canecas, etc., se vierte el contenido de otro volumen elegido como unidad y contamos las veces que sea necesario repetir esta operación. El volumen medido así recibe el nombre de capacidad.
Los conceptos de volumen y capacidad están tan, que podemos considerar que esta última corresponde al volumen interior de un cuerpo hueco.
Es decir en un cuerpo hueco podemos considerar dos volúmenes; el exterior y el interior. El exterior corresponde al volumen del recipiente y el interior es propiamente, la capacidad, y la diferencia entre los dos corresponderá al espesor de las paredes del recipiente.
Procedimiento
Primer paso: Calcular cuántos cubos de azúcar de 1 cm3 completan una capa de centímetros cúbicos en el decímetro cúbico.
¿Cuántos centímetros cúbicos se necesitan para completar un decímetro cúbico? ¿Qué concluye?
Respuesta: 100 cubos de 1 cm3, completan una capa de 1 dm3, por consiguiente, 1.000 cm3 equivale a 1 dm3.
TALLER: Midiendo la capacidad de recipientes
Teoría: La unidad métrica de las medidas de capacidad es el litro. éste tiene múltiplos y submúltiplos tales que cada unidad equivale a diez veces la unidad inmediatamente inferior.
Objetivos : Determinar la capacidad de diferentes recipientes usando números enteros y unidades.
Comprobar que un decímetro cúbico es igual a un litro.
Materiales:
Jeringas de diferentes tamaños.
Vasos de diferentes tamaños.
Una botella de gaseosa litro y una pequeña.
Lápiz y borrador.
Pecera con mediadas de 1dm. por cada arista.
Hacer grupos de nueve personas.
Pasos a seguir:
Toma una de las jeringas y llénala de agua, deposita en el cubo el agua hasta llenarlo. ¿Cuántas jeringas necesitaste para llenar el cubo?
Toma uno de los vasos y llena el cubo de la misma forma y observa cuántos vasos de agua necesitaste para llenarlo.
Haz lo mismo con la botella pequeña. Cuántas botellas de agua necesitaste esta vez.
Llena la botella litro de agua y deposítala en el cubo.
¿Qué observas?
¿Qué equivalencias encuentras?
¿Qué concluyes?
Observaciones
La capacidad de la pecera equivale a 20 jeringas de agua, cuatro vasos de agua, una botella litro de agua y casi tres botellas de gaseosa pequeña.
Un decímetro cúbico del volumen de la pecera equivale a un litro de capacidad.
En el taller se observa que los estudiantes escogen una magnitud, la capacidad y seleccionan un objeto que tiene la propiedad a medir.
Establecen unidades de medida estandarizadas y no estandarizadas.
Formulan pasos a seguir para un proceso de comparación entre la unidad establecida y la propiedad del objeto.
Concluyen asignando un número con su correspondiente unidad para representar la medida, en este caso, la capacidad de la pecera.
Adicionalmente, experimentan con la equivalencia entre un decímetro cúbico y un litro.
Para terminar esta presentación de talleres, vale la pena observar:
A. Una conclusión sobre equivalencia entre 1dm3
y 1 litro, abordada por los estudiantes en varios talleres.
B. Los estudiantes, en estos talleres planteados en la asignatura de matemática, presentan una serie de ejercicios prácticos que se solucionan con factores de conversión utilizando unidades de medida arbitrarias, así:
Si quince dulces es la medida del espacio de una caja de casetes, ¿cuál es la medida del espacio de una caja de cartón utilizando como unidad de medida los dulces, teniendo en cuenta que en la caja de cartón caben 5 cajas de casetes?

Concatenado a este manejo en matemática y teniendo como presupuesto que esos conceptos son una herramienta básica para la aplicación en unas de las temáticas de la asignatura Química I, cada uno de los ejercicios planteados por el docente de Química o los estudiantes se diseñan con el fin de analizar los procesos de medir utilizados.
Es así como alrededor de la primera conclusión (A) que se presentó en matemática, en Química se realizó una experiencia práctica solicitándoles a los estudiantes diseñar y elaborar un cubo de 1 dm3 (decímetro cúbico), procediendo a llenarlo de agua, utilizando para ello un objeto graduado que les permitiera medir la cantidad de líquido utilizada para llenar el recipiente. Posteriormente, la experiencia se repitió en el aula en grupos de cinco estudiantes y en cada grupo se realizó una puesta en común para establecer formalmente la equivalencia entre 1 dm3 (decímetro cúbico) y 1 l (un Litro) de agua. Simultáneo a este trabajo, se realiza la experiencia con el cm3 (centímetro cúbico) para medir su capacidad en ml (mililitros), llegando también a establecer la equivalencia con cada grupo entre 1cm3 y 1 ml.
Vale la pena anotar que después de realizada esta experiencia, los estudiantes, siempre que necesitaban resolver problemas o ejercicios relacionados con capacidad o con volumen, recurrían a anotar y a utilizar la equivalencia.
Finalmente, a través del establecimiento de las equivalencias matemáticas, se concluye la relación entre unidades de volumen y unidades de capacidad, dado que experimentalmente se manejan indistintamente unidades de ambas magnitudes.
Alrededor de la conclusión B para la experiencia en química, los ejercicios que se diseñaron requieren del uso de factores de conversión, factores que de hecho implican el uso de la proporcionalidad y la idea de medida. El docente de química aborda la temática con ejercicios similares a aquellos planteados en semestres anteriores, pero cambia el enfoque de la mirada para indagar en las estrategias utilizadas por los estudiantes y en las respuestas dadas, los elementos que ellos trasladan desde las ideas trabajadas, en medida, en matemáticas y su utilización en química.
Una muestra de los ejercicios desarrollados por los estudiantes en química se examina a continuación:
¿Cuántos mililitros de bromo se deberán tomar para obtener 34,0 g del mismo elemento?
En el desarrollo de este ejercicio, los alumnos proceden a buscar la densidad del elemento en la tabla periódica; este dato lo toman y empiezan a utilizarlo sin unidades, situación que contrasta con el concepto de medir que ha sido estudiado previamente en matemáticas como ya se señaló.
Procedimiento observado:
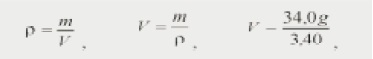
Se nota que el resultado sí es registrado con unidades de volumen, las cuales no son utilizadas en el procedimiento. En otros casos, cuando se plantea un ejercicio, se lleva a cabo el procedimiento pero la respuesta la registran sin unidades. Ejemplo: Expresar 35 mg en Kg.
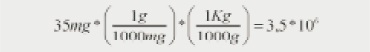
Es notoria aquí la operatoria numérica en la cual enfatiza el estudiante, sin llegar a poner el acento en medición, lo cual implicaría como centro de atención la transformación de las unidades.
Sería interesante observar y analizar de manera sistemática por qué la mayoría de estudiantes no presentó dificultades al trabajar con unidades arbitrarias, pero sí con unidades estandarizadas, y eso muy posiblemente nos lleva, entre otros, a la complejidad del sistema en base diez.
Consideramos que hizo falta una etapa de entrevistas a los estudiantes que permitieran indagar en profundidad sobre sus respuestas a los cuestionarios iniciales, vacío que se detectó cuando ellos ya habían elaborado la lectura y, por lo tanto, muy posiblemente sus respuestas eran diferentes a las pensadas en el momento de llenar los cuestionarios.
Los talleres elaborados por los estudiantes, y de los cuales se presenta un ejemplo sobre capacidad, permiten observar que se ha logrado un mayor acercamiento a entender la medición como un proceso y dentro de dicho proceso, se han identificado claramente elementos como: magnitud, unidad de medida, comparación, asignación de un número para representar la medida, sin que con ello se sugiera que se llega a una conceptualización de magnitud y cantidad.
Experiencias como la llevada a cabo en el proceso aquí descrito, realizadas en los primeros niveles de escolaridad, generarían la posibilidad de alcanzar matemática y experimentalmente el concepto de medición en niveles superiores, el cual no se convertiría solamente en un manejo de ecuaciones sino en una comprensión del proceso que lleva a la medida.
1. Arce J, Castrillón G, Soto C. Geometría 6. Serie Actividad Matemática. 2a ed. Cali: Universidad del Valle, Facultad de Educación; 1992
2. Brown Le May B. Química: La ciencia central. 7a ed. 1990.
3. Cambell, N. Medición. En: Newman J compilador. Sigma: El mundo de la matemática. Vol. 5 Barcelona: Grijalbo; 1969. p. 186-201.
4. Chamorro M, Belmonte J. El problema de la medida. Editorial Síntesis; 1991.
5. Chevallard Y. La transcripción didáctica del saber sabio al saber enseñado. Grenoble: Editorial Savvages; 1985.
6. Malone L. Introducción a la Química. 1993.